What Is Binary Search And How It Works In Data Structure?

When we develop any application, we need to store application data. We can store application data by using a linear and non-linear data structure.

But the problem is how to search any element in a given dataset and which data searching method is best for any specific dataset.

To solve this problem, we should have a good knowledge of data structure. However, there are many data searching techniques available. But we are going to discuss the binary search. which is faster than a linear search algorithm?

Pre-requirement to implement binary search

1. Sorted list: We are going to use selection sort acts as follows: you look through the whole array for the tiny element, once you find it, you exchange it with the first element of the array. Then you see for the tiniest element in the remaining array (an array without the first element) and swap it with the next element. Then you look for the tiniest element in each remaining array (an array without first and second elements) and interchange it with the third element, and so on, For example.
2. Number of steps to find Required data: How many levels will waste to retrieve data?.

What is Binary Search?

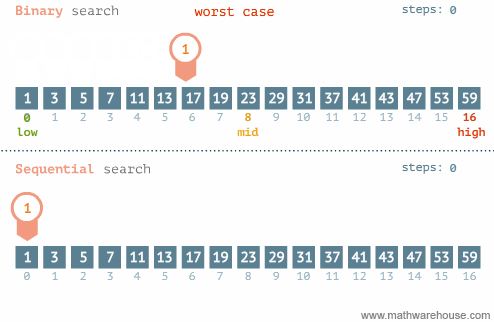
A binary search is known as a half-interval search because it divides large problem into a small problem. we use the algorithm in computer science to locate a particularised value (key) inside an array. For the exploration to be binary, the array needs to be sorted in either ascending or descending order.

How does binary search works

How does Binary search works?

Binary search divides the massive downside into a little downside. First, it divides the list into the two-part as associate degree interval. It Compares to the target value from the centre worth.

If the target value is similar to the centre value, then the binary search can terminate the method and it’ll print the desired component.

If not found, then it’ll ensure the desired knowledge is a smaller amount than the centre worth or larger than middle worth. If greater, the looking method can continue on the proper right side of the centre worth. Otherwise, it’ll search for the left look of the centre worth.

The time complexity of the binary search

Time complexity indicates how many steps will spend to obtain target data from a list, is called time complexity. We can calculate the time complexity by the formula, olog(n).

But actually we can say Olog(n) as log2n because the base of the log doesn’t involve. So beginning sees illustrate how log2n works.

Expression: log₂(n)

– – – – – – – – – – – – – – –

For n = 2:

log₂(2¹) = 1

Output = 1

– – – – – – – – – – – – – – –

For n = 4

log₂(2²) = 2

Output = 2

– – – – – – – – – – – – – – –

For n = 8

log₂(2³) = 3

Output = 3

– – – – – – – – – – – – – – –

For n = 10

log₂(2⁵) = 5

Output = 5

• So finally binary search will need 5 steps to find required value,

Because  n=10 =log2(25) = 5.

Binary search algorithm

We hope you understand how binary search works. now it’s time to write an algorithm for binary search. you can implement this algorithm in any programming language.

• Step 1: [INITIALIZE] SET BEGINNING = L    // ‘L’ is used for lower value//
• SET END = R,                                         //R is used for higher value.//
• POS = – 1                                            // we use ’-1’ to stop iteration//
• Step 2: Repeat Steps 3 and 4 while BEGINNING <=END
• Step 3: SET MID-VALUE = (BEGINNING  + END)/2
• Step 4: IF A [MID-VALUE] = VAL   //VAL is used for target value or required data.//
  SET POS = MID-VALUE
  PRINT POS
  Go to Step 6
  ELSE IF A [MID-VALUE] > VAL
  SET END = MID-VALUE – 1
  ELSE
  SET BEGINNING = MID-VALUE + 1
  [END OF IF]
  [END OF LOOP]
• Step 5: IF POS = -1
  PRINT “DATA IS NOT AVAILABLE IN THE LIST,”
  [END OF IF]
• Step 6: EXIT

Summary

Binary search has decreased time to find data in an array. There are different methods for searching and sorting in the data structure. These methods we can perform according to data’s nature.